RSA/SHA加密和数字签名的使用

RSA/SHA加密和数字签名的使用

马草原 962 2022-05-07

RSA/SHA加密和数字签名的使用

加解密、加验签在金融系统中十分普遍，最近再搞金融业务，前来学习一下。

加密算法

加密算法分为两大类：

  • 对称加密算法
  • 非对称加密算法
密钥个数 加密 解密
对称加密 一个 使用密钥加密 使用同一个密钥解密
非对称加密 两个,公钥和私钥 使用其中一把密钥加密 使用另外一把密钥解密

RSA非对称加密算法

  • RSA是目前应用最广泛的非对称加密算法，各种语言都支持RSA算法，如Java,Python,C++,Go,PHP,JavaScript等。

  • 对于一个私钥匙、有且只有一个与之对应的公钥。公/私钥的主流可选位长度为1024、2048、3072、4096…，越长安全系数越高。私钥加密的内容，使用公钥能够解密，同样使用公钥加密的内容，使用私钥也能解密。

  • 在Linux系统下，有两种常用的工具生成RSA密钥对，ssh-keygen和openssl genrsa。

  • RSA是一个能够同时用于加密和数字签名的算法，典型的应用场景：隐藏原文、防止原文被篡改、身份认证。隐藏原文是所有加密算法的通用功能(要不然怎么叫加密)，防止原文被篡改是数字签名的功能，数据传输的具体流程如下：

  1. 甲方构建密钥对，将公钥交给乙方
  2. 甲方使用私钥加密原文，然后将加密数据发送给乙方。乙方使用公钥对签名进行解密，获取原文，如果解密失败，则原文被篡改。
  3. 乙方给甲方发送原文的时候，先使用公钥对原文加密，将加密数据发送给甲方。甲方使用私钥对签名解密，获取原文，如果解密失败，则原文被篡改。

  • 如果第三方不知道密钥对，则第三方什么都做不了。如果第三方知道公钥，则第三方对甲方的原文具有与乙方一样的阅读权限，但无法篡改甲方的原文，因为没有私钥，无法生成合法的数字签名。

  • RSA对一次加密的明文的长度是有要求的，在不同的padding模式下，能加密的明文长度也不相同。以RSA 1024为例，输入的明文的字节数不能超过钥模长1024bits，即最长为128bytes。RSA 1024的不同padding模式下的明文长度的最大值计算公式：

    1. RSA_PKCS1_PADDING RSA_size(1024) - 11 = 117bytes
2. RSA_PKCS1_OAEP_PADDING RSA_size(1024) - 41 = 87bytes
3. RSA_NO_PADDING  RSA_size(1024) = 128bytes

  • 由于RSA等非对称加密算法对原文长度有限制，且算法效率没有对称加密高，在实际应用中通常被用于传递对称加密算法的密钥（通常是一个随机值），然后通信双方使用对称加密算法保证数据安全。

数字签名

数字签名是一份数据经过特定的算法计算后得出的特殊标识，用来防止数据在传输过程中被伪造或篡改，是非对称加密技术与数字摘要技术的综合应用。

数字摘要

  • 数字摘要指可以将任意长度的数据，通过一个摘要算法计算得到的固定长度的数据。也就是说摘要算法可以将很长的数据变为一个固定长度的数据，通常计算得出的数据要比原始数据短得多，所以被称为摘要，典型的摘要算法有MD5和SHA1。
  • 数字摘要算法具有以下重要特性： 1. 原数据不同，计算得到的摘要一定不同，反之，原数据不变，计算得到的摘要一定相同。 2. 无法通过摘要逆运算获得原数据，即摘要计算不可逆。 3. 任意长度的输入数据，经过计算都会得出固定长度的摘要。

加密算法和摘要算法的区别

  • 加密后的密文可以使用对应的密钥进行解密，获取原文;摘要是不能进行逆向解密的
  • 加密之后的密文的长度不定；摘要的长度是确定的
  • 非对称加密对明文的长度有限制；摘要对明文长度无限制

应用场景

  • 非对称加密技术能够确保只有持有密钥对的双方才能获取到正确的数据，但对加密原文的长度有限制，而数字摘要算法能够将输入数据转换为固定长度的摘要，并保证在原数据不变的情况下，摘要计算结果是一致的。这两项技术的特性的结合，就形成了数字签名的经典应用场景：
  1. 发送者使用MD5(或SHA1)算法提起原文摘要，然后使用私钥对摘要进行加密，把密文与原文一起传送给接收者。
  2. 接收者使用公钥对密文进行解密，获得摘要，然后使用与发送者一样的摘要算法MD5(或SHA1)对原文提取摘要，比较两个摘要是否相等
  3. 摘要相等，说明原文完整且没有被篡改；不相等，说明原文不正确。
  • 数字签名有两种作用：1. 在私钥没有泄漏的情况下，能够确保数据是由发送方签名发送的。 2.能够确保数据是完整的且没有被篡改。但是数据本身是否加密，并不是数字签名的作用范畴，因为加密的是摘要，并不是数据本身。

RSA和数字签名在第三方开放平台中的应用

在第三方开放平台中，RSA和数字签名多用于开发者接入的身份验证。如云信通IM（QQ）、网易云信、融云等开放平台的开发者接入鉴权都使用了RSA算法或数字签名作为鉴权体系的核心算法。

RSA的应用

  • 独立开发者接入平台时，使用RSA算法作为开发者身份验证的核心算法，如云信通IM平台即使用此种模式。开发者接入平台时，需要如下几个步骤：
  1. 创建一个应用app，平台会分配一个SDK_APP_ID
  2. 将SDK_APP_ID关联到一对RSA的公钥和私钥上，公钥和私钥由平台生成
  3. 由云信通IM平台持有公钥，开发者持有私钥
  4. 开发者的服务每次调用平台接口时，需要携带使用指定参数和私钥生成的签名，生成签名的公式为：RSA(私钥,SDKAPPID,用户id)
  5. 云平台会验证每次接口调用中传入的签名和用户ID，首先使用公钥对签名解密，然后验证SDK_APP_ID是否合法，比对用户ID，保证用户ID不会被篡改。
  6. 每个签名具有默认的有效期，也就是说，在私钥不变的情况下，一个用户的签名在有效期内是可以反复使用的
  • 在独立开发者接入平台的场景中，开发者自己需要保证私钥的安全，且用户登陆的验证由开发者的后端服务来执行，平台并不负责验证用户是否登陆，平台仅需要验证服务的调用方是否是合法的开发者。经典的交互流程如下所示：
    sign

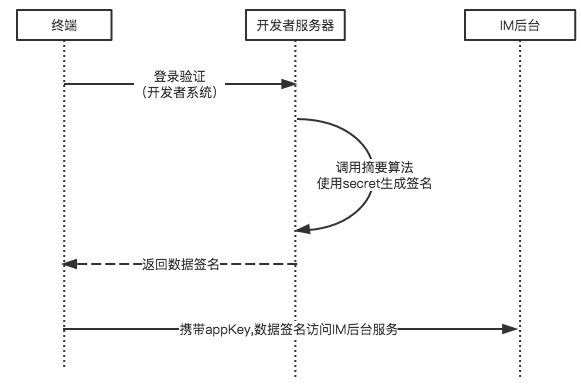
数字签名的应用

SHA1哈希算法生成数字签名也被应用于独立开发者接入模式，如融云开放平台、网易云信就使用此模式。开发者接入平台时，需要如下几个步骤：

  1. 开发者申请接入平台，由平台分配AppKey和Secret，Secret由开发者确保安全
  2. 在所有平台服务端 API 接口的请求中，都需要附带以下4个HTTP Request Header：
    | 名称| 类型 | 说明 |
    | AppKey | String | 平台分配的 App Key |
    | Nonce| String | 随机数，长度无限制 |
    | Timestamp | String | 时间戳 |
    | Signature | String | 数字签名 |
  3. 数字签名是用于检验开发者是否合法的关键，其生成方式为：App Secret、Nonce (随机数)、Timestamp (时间戳)三个字符串按先后顺序拼接成一个字符串并进行 SHA1 哈希计算。
    这种开发者接入模式中，数字签名起到几个作用：
  4. 用于验证开发者的合法性
  5. 用于保证关键参数如AppKey，Timestamp不被篡改（前提是开发者保证了Secret的安全）
  6. SHA1没有明文长度的限制，这也是其比RSA算法有优势的地方，但SHA1算法是摘要算法，其计算出来的结果是无法解密的。

运维支持

不管是使用RSA加密算法，还是SHA1等摘要算法作为核心算法，均需要建立一个稳定、易用的运维平台，支撑整个开发者接入和维护的完整生命周期。

整个运维平台需要支持的事情不限于

  1. AppKey和Secret的生成（SHA1）、Secret修改、失效
  2. 公钥和私钥的生成（RSA）、添加、失效
  3. 开发者帐号流量监控、报警、限流等
    …
知识 技术 分享